The toddler’s introduction to Heap exploitation (Part 2)
In my last post I had been talking about the heap structure in the context of the ptmalloc allocator. I went through some basic concepts, like the arena, the sub-heaps and the chunks and I used a real life example to simplify these concepts and (hopefully) help with memorising them. In this part, I am going to focus on the aftermaths of the free function, focusing on how the allocator manages the released memory in the most effective way.
Freeing a chunk
Recall from part 1, that when a chunk is in use it carries within, information about its size as well as three more flags represented by the last three bits of the number that indicates the size (we named them |A|M|P|). As the chunk size is always 8-byte (for 32 bit system) or 16-byte aligned (for 64 bit system) , these last bits are ignored during the size calculation, thus the binary value 1111 (binary) will still count as 8 bytes. The three last bits indicate if the chunk comes from the main arena, if it was allocated using a call to mmap and if the previous chunk is in use. With this information in hand and since the chunks are adjacent to each other in memory, if someone knows the address of any chunk in the heap, then it is possible to iterate through all of them using the value indicated by the size.
When the function free is called the allocator will first perform a sanity check to verify the validity of the chunk (eg. alignment, boundaries, if is already free etc.) and if everything checks out it will use the (now) unused data area to store the values depicted below:

Please pay attention to the the FWD and BCK pointers as their values are going to be used in order to integrate the chunk into a list called bins.
A Real Life Example: Back to our parking model, what we have seen so far is that when Alice finds a suitable free space for an incoming car, she removes it from her availability list and gives a ticket to the driver. This ticket contains how many slots the car can occupy as well as info about the arena, the adjacent slots and if the it belongs to an extended area (remember, if Alice can’t find a slot she can request the company to extend the parking). On the way out, she receives the ticket back and she has to add the place back to her availability list.
As she uses a simple notebook, she struggles every time to find a place with the right size and she has to search page by page in order to find an appropriate one. To avoid cars accumulating in the parking queue she has to figure out a way to accelerate the process and this is what we are going to see next.
Alice’s Binning
When Alice receives a parking ticket from an outgoing vehicle, she adds it to her unsorted pile with the hope that the number of slots on it will match an upcoming parking requirement. If this doesn’t happen she puts it in a shorted “pile” in the surface of her office. This way she will be able to trace it fast and assign it to an incoming vehicle.
To visualise Alice’s solution we can thing of the tickets as playing cards in a solitaire game, where each card is added to a specific pile according to some specific characteristics. She can have only 64 piles in this office where each pile can have 7 cards. Now, think of an incoming car that must occupy 2 parking slots. Alice, simply has to pick up the first ticket from the 2-slot pile and give it to the driver:

When there is no more space in a pile or she can’t create a new one, she uses a specially designed cabinet called Fastbins to archive the tickets. Each drawer refers to a size of x parking slots, for example the first drawer contains the 1slot tickets, the second the 2slot and so on, thus it is easy for her to keep again track of the parking slots very effectively.

On busy days, she has to be more creative as the solutions described above do not suffice. So she uses two storage boxes. In the first one (small bins) she puts the tickets up to a specific size and each sub-box contains tickets of one size. In the second (large bins) she puts the tickets of large size and each sub-box contains tickets of specific range:

With this in mind, let’s see how ptmalloc‘s corresponding binning.
Ptmalloc’s Binning
We are at the point where the free function has been called and the freed chunk has to be indexed for future reuse. The FWD and BCK pointers that were added in the data section (remember the difference between a free and used chunk) will be used to integrate the chunk to a doubly or singly linked list:


But how effective would it be if every free chunk, despite the size, was integrated in one list ?
Similarly to Alice’s simple notebook approach, the allocator has to iterate the list of free chunks to find one that satisfies a memory request. As you understand this would be highly ineffective for large number of allocations. To tackle this problem the allocator maintains a series of lists called bins and uses them to index the chunks according to their size. Ptmalloc uses 5 types of bins: tcache, fast, unsorted, small and large:

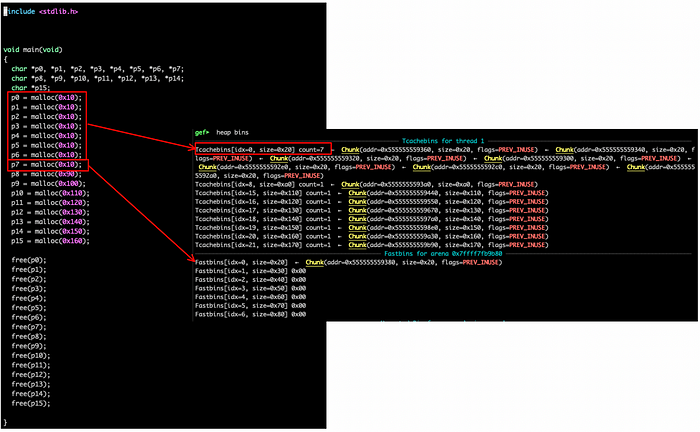
tcache: contains singly linked bins of chunks that belong to a single thread. Each bin contains one size chunk, so the array is indexed (indirectly) by chunk size. For example if we invoke malloc 8 times to allocate 0x20, 0x20, 0x30,0x30,0x40, 0x40,0x50,0x50 bytes, the tcache will look as bellow:

The number of chunks for each bin is thresholded by the tcache_count variable and the number of bins by the tcache_bins [1]:
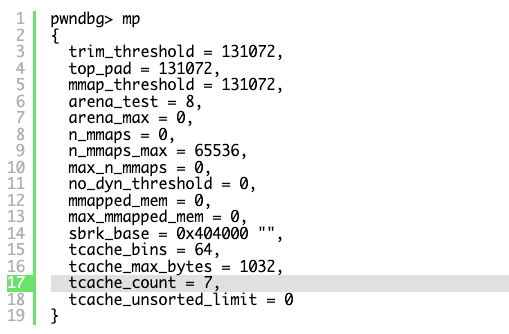
So if we allocated 0x20 bytes more than 7 times, another bin bucket will be called to facilitate the chunk. For example 9 allocations of 0x20 bytes yields the following heap arrangement:

Fastbins: An array of lists holding recently freed small chunks. Fastbins are not doubly linked. It is faster to single-link them, and since chunks are never removed from the middles of these lists, double linking is not necessary. Also, unlike regular bins, they are not even processed in FIFO order (they use faster LIFO) since ordering doesn’t much matter in the transient contexts in which fastbins are normally used [1].
It is actually, an array of pointers where each one of them points to the top of a singly linked list that contains chunks of a particular size (16, 24, 32, 40, 48, 56, 64, 72, 80, and 88 bytes plus the chunk’s metadata):
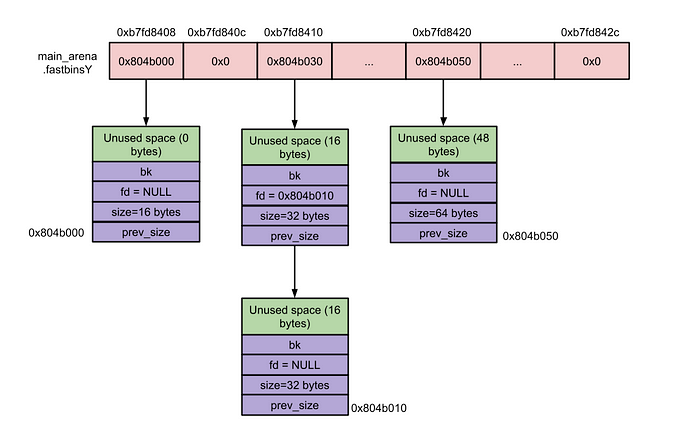
So, let’s say that there is a malloc request for 32 bytes, then the allocator will refer to the entry at address 0xb7fd8410, it will remove the top chunk (the first in the list) and will set the pointer to the second entry. To understand the swap from tcache to fastbins see the figure below:
Small bins: There are 62 of them, and each small bin stores chunks which have the same (fixed) size. Every chunk less than 512 bytes on 32-bit systems (or than 1024 bytes on 64-bit systems) has a corresponding small bin. Since each small bin stores only one size of chunk, they are automatically ordered, so insertion and removal of entries on these lists is incredibly fast [2].Small bins are doubly-linked so that chunks may be removed from the middle.
Large bins: There are 63 of them and the main difference with the small ones but instead of storing chunks with a fixed size, they instead store chunks within a size range [1].
More specifically ptmalloc defines[3]:
- 32 bins for storing chunks of size which are 64 bytes apart. So, bin[64] will contains doubly linked structs (malloc_chunk) of size between 512 to 568, bin[65] of size 576 to 632, bin[66] of size 640 to 696 and so on…
- 16 bins for storing chunks of size which are 512 bytes apart.
- 8 bins for storing chunks of size which are 4096 bytes apart.
- 4 bins for storing chunks of size which are 32768 bytes apart.
- 2 bins for storing chunks of size which are 262144 bytes apart.
- 1 bin contains a chunk of remaining size.
Unsorted bins: When chunks are free’d they are initially stored in a single bin (doubly linked). They’re sorted later, in malloc, in order to give them one chance to be quickly re-used. This also means that the sorting logic only needs to exist at one point — everyone else just puts free’d chunks into this bin, and they’ll get sorted later. The “unsorted” bin is simply the first of the regular bins [4].

That’s all for this post ! See you in the next one.
References
[2] https://azeria-labs.com/heap-exploitation-part-2-glibc-heap-free-bins/
[3] https://sploitfun.wordpress.com/2015/02/10/understanding-glibc-malloc/

